En este método es muy importante saber como debemos utilizar las variables:
Para ilustrar la técnica de las variables artificiales, primero se considerará el caso en que la única forma no estándar en el problema es la presencia de una o más restricciones en forma de igualdad.
Aplicando la técnica de las variables artificiales se introduce una variable artificial no negativa (denotada por x5) en la última ecuación, como si fuera una variable de holgura:
3x1 + 2x2 + x5 =18
En resumen si tenemos una restricción funcional en forma de igualdad y deseamos “pasarla a su forma de igualdad”, únicamente debemos sumar una variable artificial.
Restricciones funcionales de la forma >-
Para ilustrar la manera en que la técnica de las variables artificiales maneja las restricciones de la forma >- usaremos el siguiente ejemplo:
Notemos que la tercera restricción es del tipo >-, por lo que para cambiarla a su forma de igualdad tendríamos que restar una variable de superávit (o de excedente), quedando de la siguiente manera:
0.6x1 + 0.4x2 - x5 = 6
Se ha restado la variable de excedente x5 (se utilizó x5 porque en la primera restricción agregamos una variable de holgura que sería x3 y en la segunda restricción agregamos también una variable artificial que sería x4; todo esto con el fin de convertir las desigualdades a su forma de igualdades) para que consuma el exceso de 0.6x1 + 0.4x2, o sea, lo que se pasa de 6. No obstante en este caso debe agregarse otra variable. Esta variable extra, llamada variable artificial se aumenta como sigue:
6x1 + 0.4x2 - x5 + x6 = 6
La razón de esto es que, si no se agrega la variable artificial, no se estarían cumpliendo las restricciones de no negatividad. Para comprenderlo, se dejará sin aumentar. El método símplex comienza por hacer todas las variables reales (originales) iguales a cero. Entonces:
0.6x1 + 0.4x2 - x5 = 6
Sea x1 = 0 y x2 = 0, entonces:
-x5 = 6
ó x5 = -6 (que no cumple la restricción de no negatividad)
La variable artificial opera para mantener todas las variables no negativas cuando 0.6x1 + 0.4x2 es menor que 6.
Si x1 = 0 y x2 = 0, entonces x5 = 0 y
0.6x1 + 0.4x2 - x5 + x6 = 6
x6 = 6
En resumen, una restricción de la forma >- se convierte a su forma de igualdad restando una variable de excedente y sumando una variable artificial.
Consideremos el siguiente problema:
0.6x1 + 0.4x2 - x5 = 6
Se ha restado la variable de excedente x5 (se utilizó x5 porque en la primera restricción agregamos una variable de holgura que sería x3 y en la segunda restricción agregamos también una variable artificial que sería x4; todo esto con el fin de convertir las desigualdades a su forma de igualdades) para que consuma el exceso de 0.6x1 + 0.4x2, o sea, lo que se pasa de 6. No obstante en este caso debe agregarse otra variable. Esta variable extra, llamada variable artificial se aumenta como sigue:
6x1 + 0.4x2 - x5 + x6 = 6
La razón de esto es que, si no se agrega la variable artificial, no se estarían cumpliendo las restricciones de no negatividad. Para comprenderlo, se dejará sin aumentar. El método símplex comienza por hacer todas las variables reales (originales) iguales a cero. Entonces:
0.6x1 + 0.4x2 - x5 = 6
Sea x1 = 0 y x2 = 0, entonces:
-x5 = 6
ó x5 = -6 (que no cumple la restricción de no negatividad)
La variable artificial opera para mantener todas las variables no negativas cuando 0.6x1 + 0.4x2 es menor que 6.
Si x1 = 0 y x2 = 0, entonces x5 = 0 y
0.6x1 + 0.4x2 - x5 + x6 = 6
x6 = 6
En resumen, una restricción de la forma >- se convierte a su forma de igualdad restando una variable de excedente y sumando una variable artificial.
Consideremos el siguiente problema:

Como explicamos anteriormente, para resolver este problema, debemos construir un problema artificial que tiene la misma solución óptima que el problema real, haciendo dos modificaciones a este problema real.
1. Se aplica la técnica de las variables artificiales introduciendo una variable artificial no negativa (denotada por x5) en la última ecuación, como si fuera una variable de holgura:
3x1 + 2x2 + x5 =18
2. Se asigna una penalización enorme al hecho de tener x5 > 0, cambiando la función objetivo
Z = 3x1 + 5x2 a:
Z = 3x1 + 5x2 - Mx5,
donde M simbólicamente representa un número positivo muy grande. Este método que fuerza a x5 hasta el nivel de x5 = 0 en la solución óptima se llama método de la M.
Nota: Para el caso de minimización, penalizamos a la variable artificial, haciéndola aparecer en la función objetivo con un coeficiente de +M.
Ahora se encuentra la solución óptima para el problema real aplicando el método símplex al problema artificial.
Como x5 juega el papel de la variable de holgura en la tercera restricción del problema artificial, esta restricción es equivalente a 3x1 + 2x2 £ 18.
En particular, el sistema de ecuaciones después de aumentar el problema artificial (en otras palabras, pasarlo a su forma de igualdades) es:
Maximizar Z, sujeta a

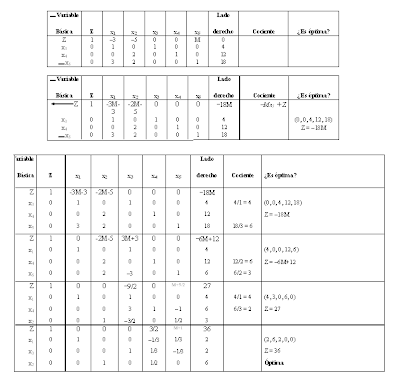
En este momento estamos preparados para pasar los coeficientes a la tabla símplex:
Método de asignación.
Este tipo de problemas tiene una gran variedad de aplicaciones dentro de la gama de la toma de decisiones. Problemas que constantemente se le presentan a los gerentes de personal, en cuanto a la colocación optima del personal; a los gerentes de producción, en cuanto a la utilización optima de equipo con diferentes porcentajes de eficiencia en relación a diferentes tareas o trabajos.
La técnica mas recomendable para solucionar problemas de asignación es la técnica de flood, que utiliza el teorema de koing, comúnmente llamado método húngaro o método de matriz reducida, en el cual a base de restas y sumas de columnas y filas después de varios ciclos se obtiene la matriz optima.
Caso practico.
PASOS:
1.-que m sea igual que n
2.-busca el menor número o costo por fila o por columna
3.-se resta el menor a toda la fila con la finalidad de llegar a cero
4.-se repite el paso anterior pero ahora por columna
5.-cuando ya hay ceros en todas las filas se hacen las asignaciones

A1=49
B1=45
C1=46
D2=38
A3=54
A4=70
Método de transporte.
El modelo de transporte busca determinar un plan de transporte de una mercancía de varias fuentes a varios destinos. Los datos del modelo son:
1. Nivel de oferta en cada fuente y la cantidad de demanda en cada destino.
2. El costo de transporte unitario de la mercancía a cada destino.
Como solo hay una mercancía un destino puede recibir su demanda de una o más fuentes. El objetivo del modelo es el de determinar la cantidad que se enviará de cada fuente a cada destino, tal que se minimice el costo del transporte total.
La suposición básica del modelo es que el costo del transporte en una ruta es directamente proporcional al numero de unidades transportadas. La definición de “unidad de transporte” variará dependiendo de la “mercancía” que se transporte.

Caso practico
Sea una empresa transnacional que tiene W, X, Y plantas y surte su producto a 7 almacenes A,B,C,D,E,F,G considerando los costos de trasporte de cada planta hacia cada almacen.
Las ventas dependen de la capacidad de cada planta.

WA=(6)(1000)=6000
WB=(7)(2000)=7000
WC=(5)(4000)=20000
XC=(4)(500)=2000
XD=(5)(2000)=10000
YD=(6)(500)=3000
YE=(5)(2000)=10000
YF=(9)(3500)=31500
YG=(4)(3000)=12000
Z=116000
Nota: es importante empezar por la esquina noroeste.

Método vogel.
Paso 1: se resta los números más bajos
Paso 2: hacer asignaciones
Paso 3: hacer los cruces

(2)(150)+(5)(150)+(2)(100)+(1)(50)+(3)(50)= 300+750+200+50+150=1450
Método dual.
Lo ocupamos cuando son mas restricciones que variables
Los pasos son los siguientes:
Paso 1: minimizar
Paso 2: pasar los coeficientes a transpuesta
Paso3: restricciones a transpuesta
Paso 4: pasar función objetivo a transpuesta
Método simplex minimizar.
Pasos:
Paso 1 se busca el mayor negativo
Paso 2: se termina cuando ya no hay negativos
Este tipo de problemas tiene una gran variedad de aplicaciones dentro de la gama de la toma de decisiones. Problemas que constantemente se le presentan a los gerentes de personal, en cuanto a la colocación optima del personal; a los gerentes de producción, en cuanto a la utilización optima de equipo con diferentes porcentajes de eficiencia en relación a diferentes tareas o trabajos.
La técnica mas recomendable para solucionar problemas de asignación es la técnica de flood, que utiliza el teorema de koing, comúnmente llamado método húngaro o método de matriz reducida, en el cual a base de restas y sumas de columnas y filas después de varios ciclos se obtiene la matriz optima.
Caso practico.
PASOS:
1.-que m sea igual que n
2.-busca el menor número o costo por fila o por columna
3.-se resta el menor a toda la fila con la finalidad de llegar a cero
4.-se repite el paso anterior pero ahora por columna
5.-cuando ya hay ceros en todas las filas se hacen las asignaciones

A1=49
B1=45
C1=46
D2=38
A3=54
A4=70
Método de transporte.
El modelo de transporte busca determinar un plan de transporte de una mercancía de varias fuentes a varios destinos. Los datos del modelo son:
1. Nivel de oferta en cada fuente y la cantidad de demanda en cada destino.
2. El costo de transporte unitario de la mercancía a cada destino.
Como solo hay una mercancía un destino puede recibir su demanda de una o más fuentes. El objetivo del modelo es el de determinar la cantidad que se enviará de cada fuente a cada destino, tal que se minimice el costo del transporte total.
La suposición básica del modelo es que el costo del transporte en una ruta es directamente proporcional al numero de unidades transportadas. La definición de “unidad de transporte” variará dependiendo de la “mercancía” que se transporte.

Caso practico
Sea una empresa transnacional que tiene W, X, Y plantas y surte su producto a 7 almacenes A,B,C,D,E,F,G considerando los costos de trasporte de cada planta hacia cada almacen.
Las ventas dependen de la capacidad de cada planta.

WA=(6)(1000)=6000
WB=(7)(2000)=7000
WC=(5)(4000)=20000
XC=(4)(500)=2000
XD=(5)(2000)=10000
YD=(6)(500)=3000
YE=(5)(2000)=10000
YF=(9)(3500)=31500
YG=(4)(3000)=12000
Z=116000
Nota: es importante empezar por la esquina noroeste.

Método vogel.
Paso 1: se resta los números más bajos
Paso 2: hacer asignaciones
Paso 3: hacer los cruces

(2)(150)+(5)(150)+(2)(100)+(1)(50)+(3)(50)= 300+750+200+50+150=1450
Método dual.
Lo ocupamos cuando son mas restricciones que variables
Los pasos son los siguientes:
Paso 1: minimizar
Paso 2: pasar los coeficientes a transpuesta
Paso3: restricciones a transpuesta
Paso 4: pasar función objetivo a transpuesta
Método simplex minimizar.
Pasos:
Paso 1 se busca el mayor negativo
Paso 2: se termina cuando ya no hay negativos